투포인터의 개념
투포인터: 두개의 포인터를 사용해 문제를 푸는 알고리즘.
1. start와 end (또는 front, back이나 left, right 등 이름은 다양하게 할 수 있다.) 두개의 포인터를 만든다.
반드시 start <= end 여야 한다. 2. 초기 두개의 포인터는 0번 인덱스를 가리키도록 세팅한다. 3. 현재 s에서 e-1까지의 합을 sum이라 하였을때 sum이 구하려는 값(m)보다 크다면 s++4. sum이 m보다 작다면 e++ 5. sum과 m이 같다면 카운트 해준다. 6. s와 e의 위치를 바꿔가면서 모든 경우를 확인한다. 정리하자면 start 시작과 end 끝을 모두 증가시켜가며 부분 배열의 합이 m인 경우를 찾는 알고리즘이다. 예를 들어 배열의 크기 n=7, 구하려는 값 m=5 일때 투포인터를 움직여보자
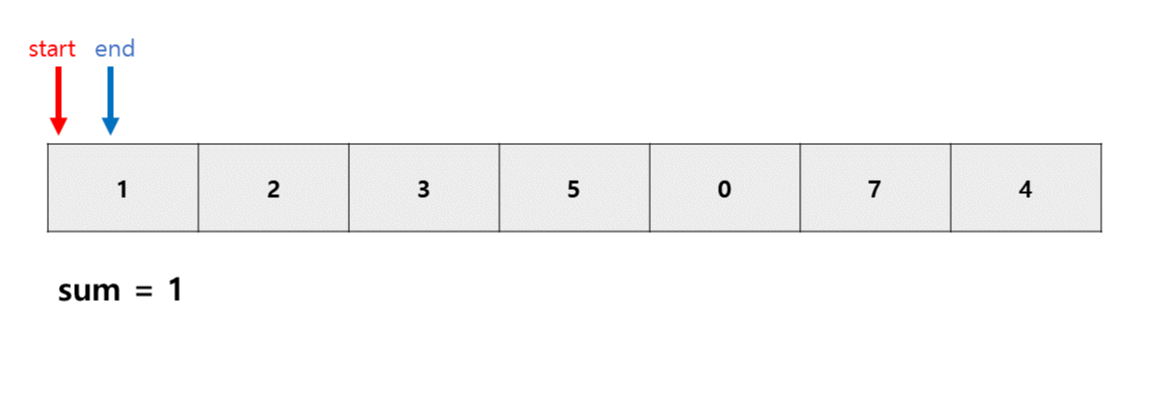
start와 end가 0번째 인덱스에서 시작한다.
0번 인덱스에서 0번 인덱스까지 더한 값은 1이므로 sum = 1이다.
sum < m이므로 end를 추가해준다.
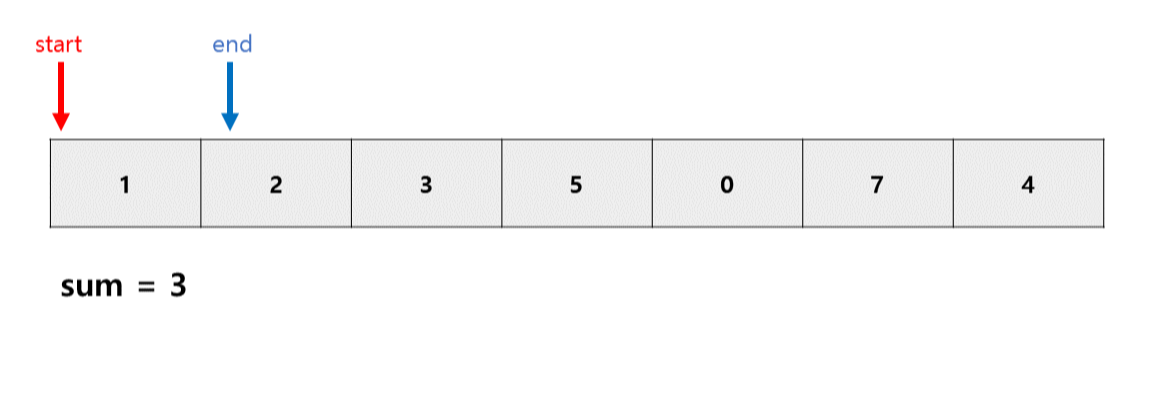
0번 인덱스에서 1번 인덱스까지 더한 값(start에서 end까지 더한 값)
sum = 3, sum < m이므로 end++ 해준다.
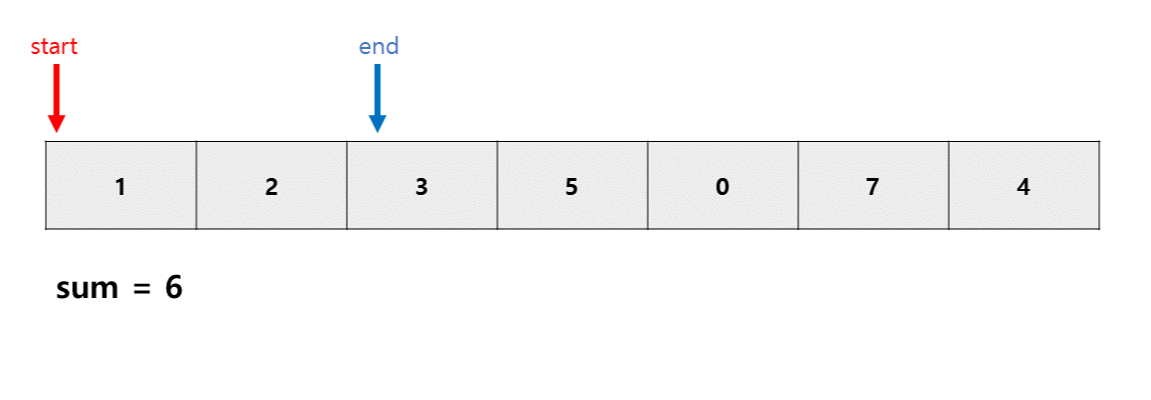
이번엔 sum > m이므로 start ++ 해준다.

sum과 m이 같으므로 카운트개수를 1 늘려준다.
그리고 같을때에도 end++ 해준다.
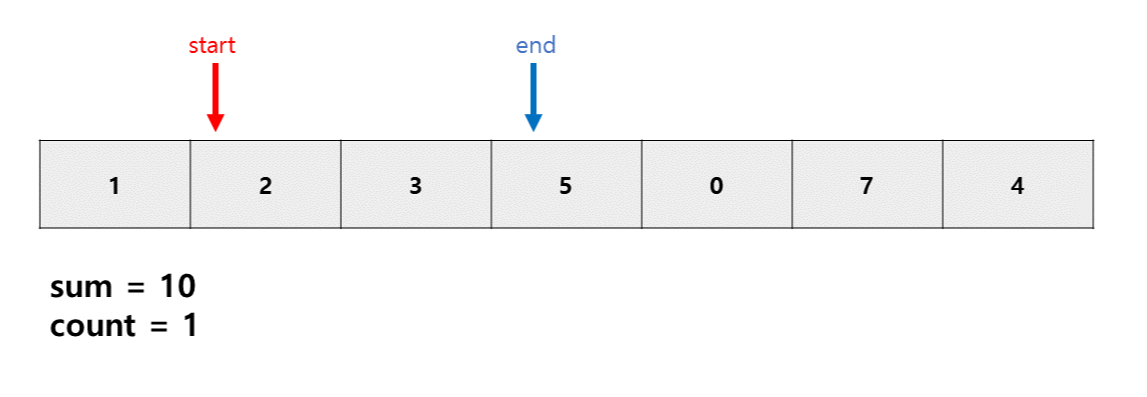
똑같이 sum >m이므로 start++
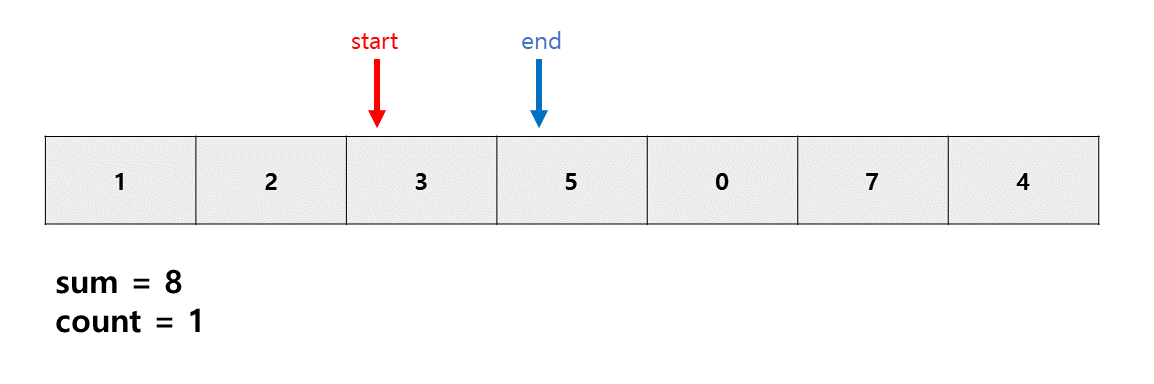
위 과정을 반복한다.
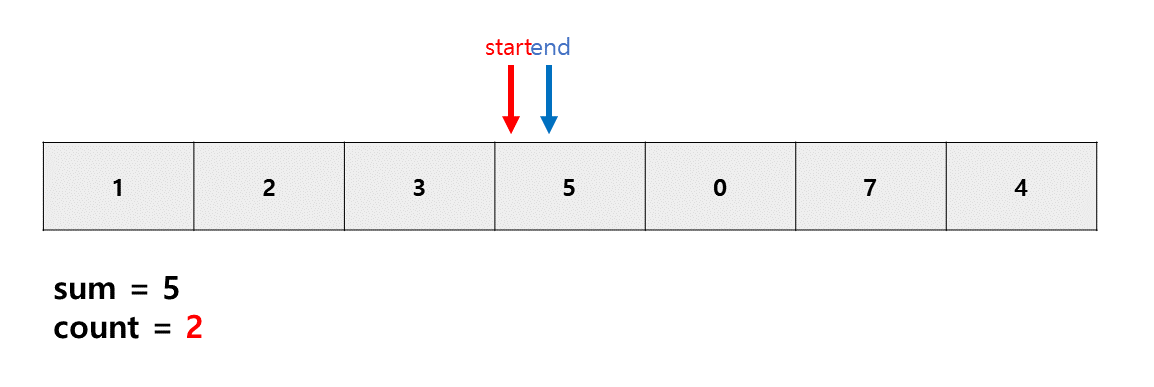
sum이 m과 같으므로 카운트 개수 늘려준다.
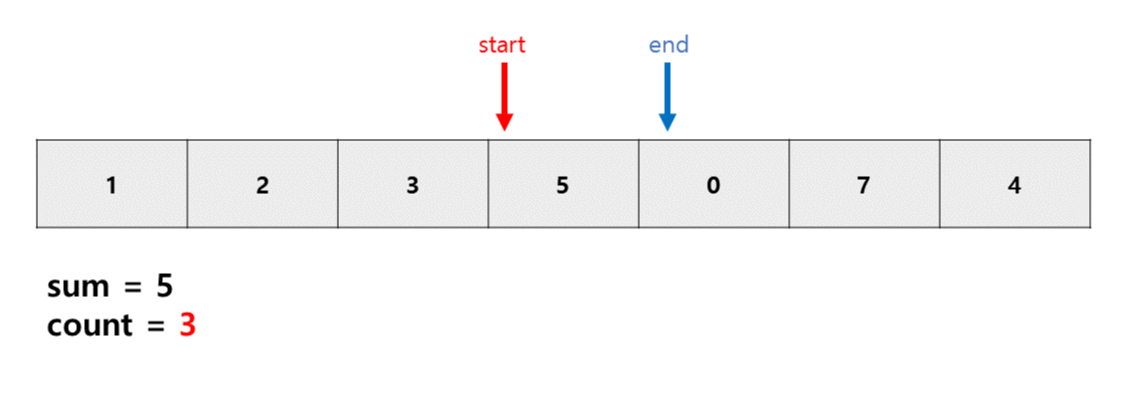
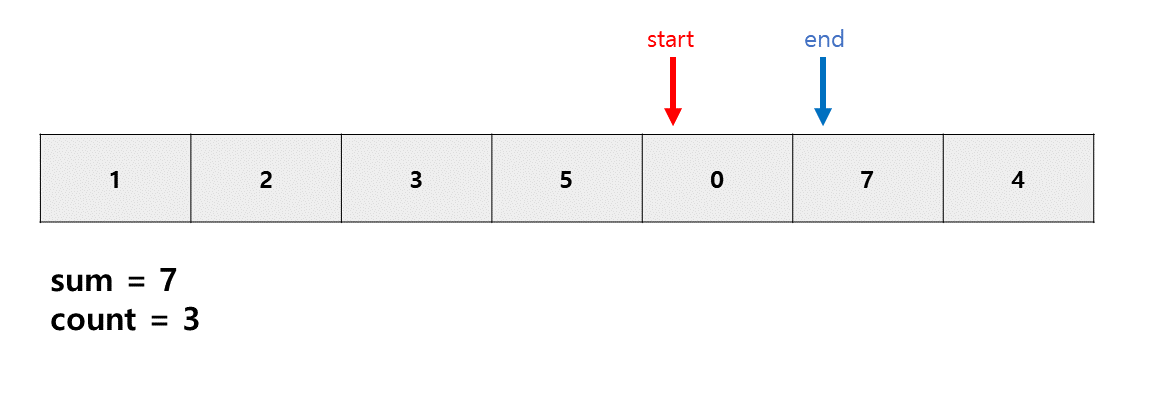
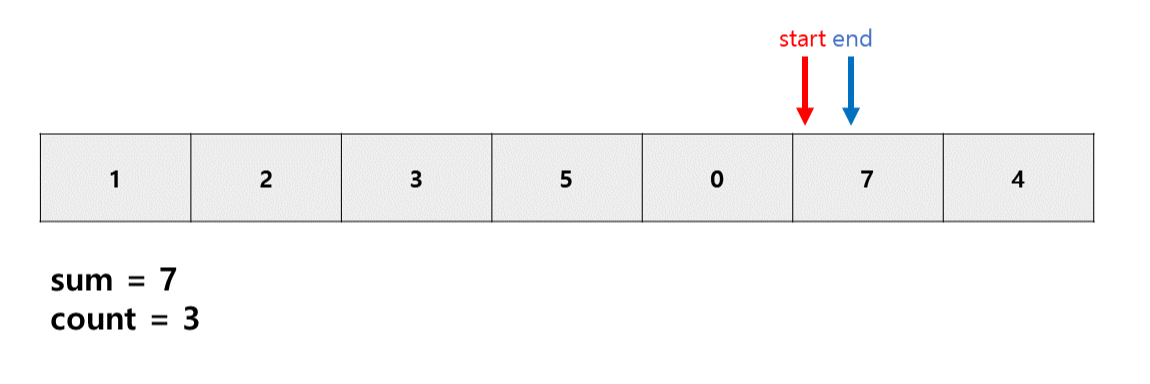
원래 sum>m인 경우 start를 늘려줘야하지만 현재 s와 e가 같다.
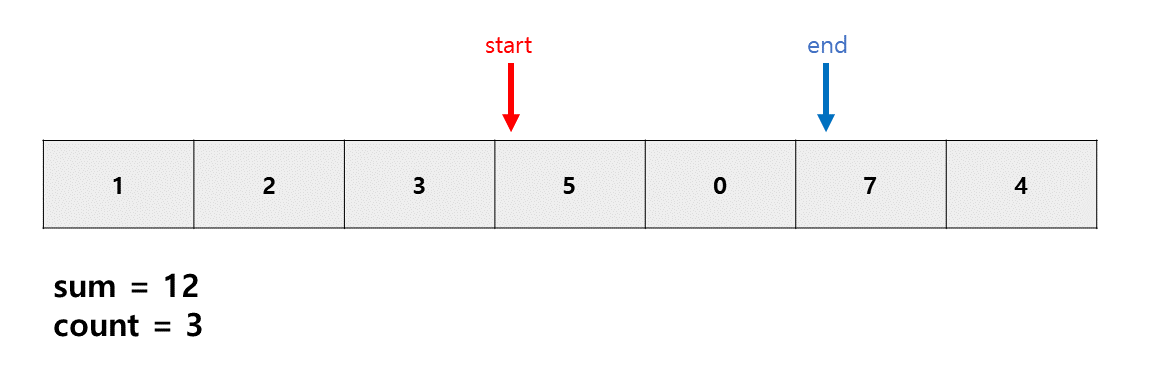
s는 반드시 e보다 작거나 같아야 되므로 s만 늘려주는 것이 아닌 s와 e 둘다 +1 해준다.
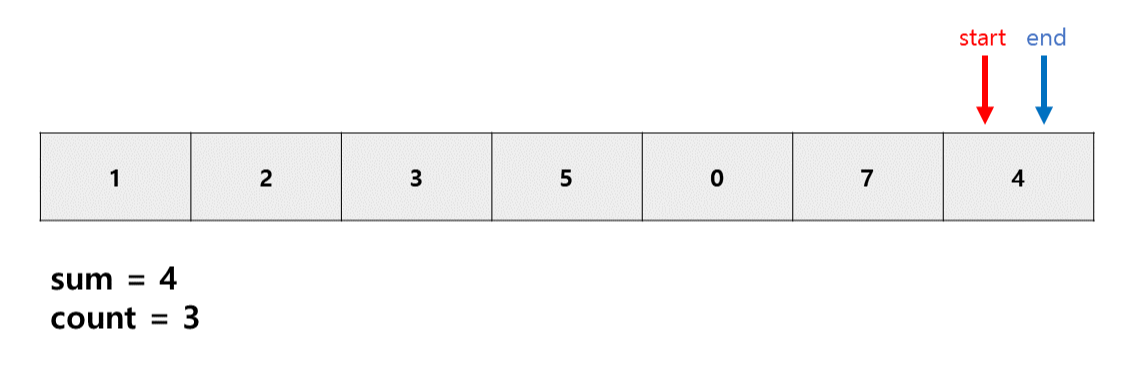
s와 e가 끝에 도달했기에 더이상 증가할 수 없는 상태가 되어 종료한다.
여기서는 s와 e가 동시에 도달했지만 보통 e만 도달하여도 루프를 마무리하거나 s가 도달할때까지 비교하는 경우도 있다.
시간복잡도
두개의 포인터가 각각 n번(배열의 크기만큼) 움직이므로 시간 복잡도는 O(n+n)이다.
즉 O(n)으로 나타낼 수 있다.
풀어보면 좋을 백준 문제
1. 2003번 수들의 합 2
2. 14246번 k보다 큰 구간
3. 2531번 회전초밥
4. 3151번 합이 0
'알고리즘 자료구조 공부일지' 카테고리의 다른 글
| [알고리즘] 유니온 파인드 (Union-Find) 개념과 최적화 기법 (0) | 2024.04.28 |
|---|---|
| 시간복잡도(Time Complexity) (0) | 2024.04.17 |
| [알고리즘] 누적합 (prefix sum) (0) | 2023.08.13 |
| [알고리즘] 재귀함수 (Recursion Function) (1) | 2023.08.08 |
| 알고리즘의 개념과 배워야 하는 이유 (0) | 2023.08.08 |
투포인터의 개념
투포인터: 두개의 포인터를 사용해 문제를 푸는 알고리즘.
1. start와 end (또는 front, back이나 left, right 등 이름은 다양하게 할 수 있다.) 두개의 포인터를 만든다.
반드시 start <= end 여야 한다. 2. 초기 두개의 포인터는 0번 인덱스를 가리키도록 세팅한다. 3. 현재 s에서 e-1까지의 합을 sum이라 하였을때 sum이 구하려는 값(m)보다 크다면 s++4. sum이 m보다 작다면 e++ 5. sum과 m이 같다면 카운트 해준다. 6. s와 e의 위치를 바꿔가면서 모든 경우를 확인한다. 정리하자면 start 시작과 end 끝을 모두 증가시켜가며 부분 배열의 합이 m인 경우를 찾는 알고리즘이다. 예를 들어 배열의 크기 n=7, 구하려는 값 m=5 일때 투포인터를 움직여보자

start와 end가 0번째 인덱스에서 시작한다.
0번 인덱스에서 0번 인덱스까지 더한 값은 1이므로 sum = 1이다.
sum < m이므로 end를 추가해준다.

0번 인덱스에서 1번 인덱스까지 더한 값(start에서 end까지 더한 값)
sum = 3, sum < m이므로 end++ 해준다.

이번엔 sum > m이므로 start ++ 해준다.

sum과 m이 같으므로 카운트개수를 1 늘려준다.
그리고 같을때에도 end++ 해준다.

똑같이 sum >m이므로 start++

위 과정을 반복한다.

sum이 m과 같으므로 카운트 개수 늘려준다.




원래 sum>m인 경우 start를 늘려줘야하지만 현재 s와 e가 같다.
s는 반드시 e보다 작거나 같아야 되므로 s만 늘려주는 것이 아닌 s와 e 둘다 +1 해준다.

s와 e가 끝에 도달했기에 더이상 증가할 수 없는 상태가 되어 종료한다.
여기서는 s와 e가 동시에 도달했지만 보통 e만 도달하여도 루프를 마무리하거나 s가 도달할때까지 비교하는 경우도 있다.
시간복잡도
두개의 포인터가 각각 n번(배열의 크기만큼) 움직이므로 시간 복잡도는 O(n+n)이다.
즉 O(n)으로 나타낼 수 있다.
풀어보면 좋을 백준 문제
1. 2003번 수들의 합 2
2. 14246번 k보다 큰 구간
3. 2531번 회전초밥
4. 3151번 합이 0
'알고리즘 자료구조 공부일지' 카테고리의 다른 글
| [알고리즘] 유니온 파인드 (Union-Find) 개념과 최적화 기법 (0) | 2024.04.28 |
|---|---|
| 시간복잡도(Time Complexity) (0) | 2024.04.17 |
| [알고리즘] 누적합 (prefix sum) (0) | 2023.08.13 |
| [알고리즘] 재귀함수 (Recursion Function) (1) | 2023.08.08 |
| 알고리즘의 개념과 배워야 하는 이유 (0) | 2023.08.08 |
