알고리즘 분석
정확성(correctness): 가능한 입력에 대해서 항상 옳은 답을 출력하는가?
자원(resources): 얼마나 많은 자원을 사용하는가?
자원은 알고리즘 실행 시간과 필요한 메모리의 양이 있다.
이 자원을 측정하기 위해 만든 것이 가상의 컴퓨터
RAM (Random Access Machine) 모델
순차적으로 수행되는 보통의 컴퓨터에 기반을 두고 있다. -> 직렬구조로 명령어가 사용된 개수에 따라 달라질 수 있다.
사칙연산, 비교, 치환 등 간단한 명령어를 가지고 있는데 이 연산을 모두 단위 시간에 수행할 수 있다고 가정한다.
실제 컴퓨터와 마찬가지로 정수의 고정된 길이(32bit, 4byte)로 표현한다
무한한 양의 메모리를 가지며, 단위 시간에 메모리에 접근할 수 있다고 가정한다
알고리즘 실행 시간은 필요한 기본 연산(명령어)의 개수로 나타낸다.
시간복잡도
입력의 개수가 n일때 알고리즘의 실행시간을 n에 대한 함수로 표현
하나의 명령어의 걸리는 시간이다.
최악의 경우 시간복잡도
입력의 개수가 n인 모든 가능한 입력에 대한 최대 실행 시간을 말한다
평균 시간복잡도
크기 n인 모든 입력에 대한 실행 시간의 평균
시간복잡도를 정확히 계산하는 것은 복잡하고 귀찮으므로 상계(upper bound)와 하계(lower bound)로 표현하는 것이 더 쉽다.
T(n)=2n^2+10n+5 라는 데이터가 있다고 하자. (여기서 T(n)은 n개일때 알고리즘 걸리는 시간, 명령어 실행 횟수이다.
n의 무수히 커질때는 n과 10n의 차이는 적어지고 n과 n^2의 차이가 많이 날 것이다.
즉, 가장 큰 데이터를 기준으로 O(n^2)으로 표현하는 것이다.
O, Ω 표기 정의
상수 c와 n0가 존재하여, n>=n0인 모든 n에 대하여 T(n) <= c*f(n)을 만족하면 T(n) = O(f(n))이라 한다.
상수 c와 n0가 존재하여, n>=n0인 모든 n에 대하여 T(n) >= c*f(n)을 만족하면 T(n) =Ω(f(n))이라 한다.
글로 설명하니 이해가 잘 안될수도 있는데 예시를 들어보겠다.
T(n)=3n^2 - 100n +6
T(n)=O(n^2)일까?
T(n)<=[ ]n^2을 n >= [ ]인 모든 n에 대하여 만족해야한다.
[ ]에 간단하게 아무 숫자나 넣어보자.
T(n) <= 100n^2 , n>=200
n이 200보다 클때 100*n^2의 경우 T(n)보다 작아진다. 따라서 O(n^2)으로 나타낼 수 있는 것이다.
그럼 T(n)=O(n)은 왜 안되는 것일까?
T(n)<=[ ] n, n>= [ ] 일때 [ ]에 들어가 충족시킬 수 있는 상수가 없기 때문이다.
이제 T(n)=Ω(n^2)를 살펴보면
T(n)>=[ ]n^2을 n >= [ ]인 모든 n에 대하여 만족해야한다.
마찬가지로 [ ]에 아무 숫자나 넣어보면
T(n) <= 1 *n^2 , n>=10000 과 같은 결과를 얻을 수 있다.
모든 n에 대하여 T(n)을 만족하므로 Ω(n^2)으로 표현할 수 있는 것이다.
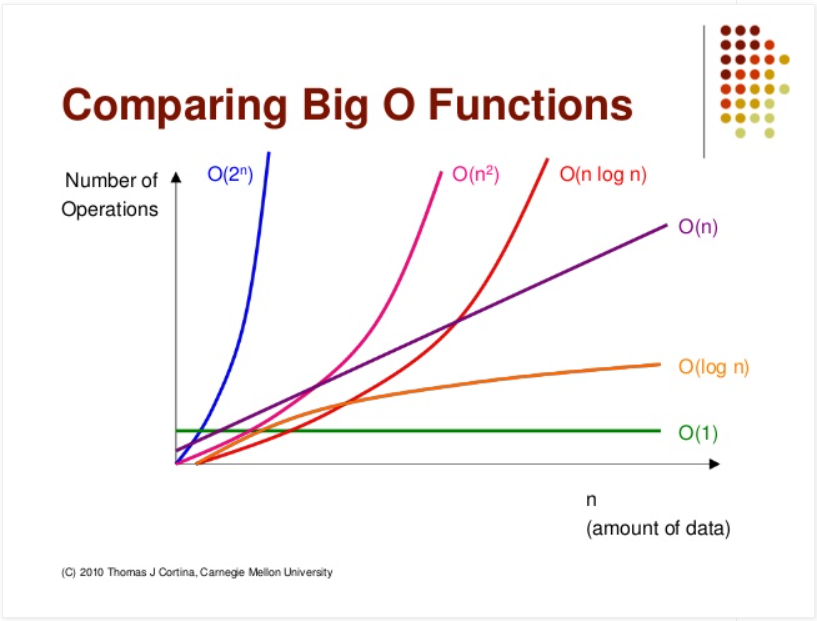
시간복잡도 분류
다항 시간(polynomial time)에 따라
𝑂(1), 𝑂(log𝑛), 𝑂(루트𝑛), 𝑂(𝑛), 𝑂(𝑛log 𝑛), 𝑂(𝑛^2), 𝑂(𝑛^3) ....
공간복잡도(Space Complexity)
추가로 공간복잡도(Space Complexity)에 대해서도 살펴보면
알고리즘이 사용하는 메모리의 양을 입력의 크기 n에 대한 함수로 표현하는 것이다.
시간복잡도와 마찬가지로 최악의 경우 공간복잡도와 평균 공간복잡도가 있다.
상계(upper bound)와 하계(lower bound)로 표현한다.
'알고리즘 자료구조 공부일지' 카테고리의 다른 글
| [알고리즘] LIS의 개념과 DP, 이분탐색을 이용한 구현 (0) | 2025.03.06 |
|---|---|
| [알고리즘] 유니온 파인드 (Union-Find) 개념과 최적화 기법 (1) | 2024.04.28 |
| [알고리즘] 누적합 (prefix sum) (0) | 2023.08.13 |
| [알고리즘] 투포인터 (Two Pointer) (0) | 2023.08.12 |
| [알고리즘] 재귀함수 (Recursion Function) (1) | 2023.08.08 |
